

Next: Grating Performance
Up: Fourier Gratings as Submillimeter
Previous: Introduction
For our application we are only interested in the far field diffraction
pattern of the gratings illuminated with a plane wave. Furthermore the
grating periods are much
larger than the wavelength, since we want to produce a closely packed
array of beams. Under these conditions we can use simple scalar diffraction
theory to model the grating performance.
The spatial phase modulation imposed by a one-dimensional Fourier grating
is given by a Fourier series expansion:
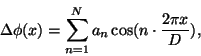 |
(1) |
where the unit cell is given by
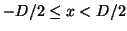 . At the moment we
restrict ourselves to symmetric, one-dimensional grating functions. The
generalization to two-dimensional gratings or
Fourier series with asymmetric components involving sine functions is
obvious. For
. At the moment we
restrict ourselves to symmetric, one-dimensional grating functions. The
generalization to two-dimensional gratings or
Fourier series with asymmetric components involving sine functions is
obvious. For 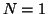 this
corresponds to the well known sinusoidal phase grating
[7],
whose Fraunhofer diffraction pattern is given by the far field distribution
this
corresponds to the well known sinusoidal phase grating
[7],
whose Fraunhofer diffraction pattern is given by the far field distribution
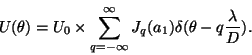 |
(2) |
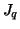 denotes the Bessel function of the first kind of order
denotes the Bessel function of the first kind of order 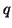 .
.
For 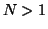 the phase modulated field in the grating plane can be written as a
product of fields modulated by the individual Fourier components:
the phase modulated field in the grating plane can be written as a
product of fields modulated by the individual Fourier components:
![\begin{displaymath}
U_0\exp[ i\Delta\phi(x)] = U_0\prod^N_{n=1} \exp[ i a_n
\cos(n\cdot\frac{2\pi x}{D})] .
\end{displaymath}](img18.gif) |
(3) |
The far field diffraction pattern ( i.e. the Fourier transform) of
this field is then given by a multiple convolution of the diffraction
fields of the individual Fourier components:
![\begin{displaymath}
U(\theta) = U_0 \times \bigotimes_{n=1}^N\left[\sum_{q=-\infty}^\infty
J_q(a_n)\delta(\theta-nq\frac{\lambda}{D})\right].
\end{displaymath}](img19.gif) |
(4) |
Although this is an elegant mathematical expression for the diffraction
pattern of the Fourier grating, for practical purposes it is usually much
faster to directly calculate the Fourier transform of the grating
structure using the numerical FFT algorithm.
Thus, through the FFT of the expression in eq. (3), the set of Fourier
coefficients 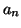 of the phase modulation
defines a set of complex coefficients
of the phase modulation
defines a set of complex coefficients 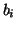 , each of which
describes the field in one diffraction order of the grating. Since we
are only interested in the intensity distribution within the
diffraction pattern, our task consists of finding a set of
, each of which
describes the field in one diffraction order of the grating. Since we
are only interested in the intensity distribution within the
diffraction pattern, our task consists of finding a set of 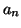 , which
produces the desired set of
, which
produces the desired set of 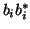 . For our standard example -- a
one-dimensional grating producing a symmetric pattern of four beams
-- this set is
. For our standard example -- a
one-dimensional grating producing a symmetric pattern of four beams
-- this set is
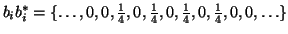 .
.
Since we cannot invert eq. (4), the coefficients
cannot be calculated directly, but an iterative method has to be
employed. FFT is so fast, even on cheap modern computers that the
following, very crude algorithm is sufficient to calculate simple
grating structures. It consists of the following two steps:
- for a given number of coefficients
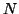 , randomly chose a large
number ( e.g.
, randomly chose a large
number ( e.g. 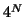 ) of parameter sets
) of parameter sets 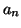 and calculate
the deviation of their respective diffraction patterns from the desired
pattern.
and calculate
the deviation of their respective diffraction patterns from the desired
pattern.
- for the few best ( e.g. 20) parameter sets, optimize the
parameter sets to minimize the deviation.
For a large enough number of starting values all or most of these
optimizations converge to the same result, which is then considered the
best approximation achievable with 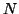 Fourier coefficients.
The first step in the algorithm prevents the global optimization from being
trapped in one of the many shallow local minima.
Fourier coefficients.
The first step in the algorithm prevents the global optimization from being
trapped in one of the many shallow local minima.
To quantify the performance of a grating we generally use
the RMS deviation of the intensity in the desired diffraction orders
from the ideal values. The optimization procedure consists in minimizing this
deviation, using a standard multidimensional minimization algorithm
[8].
The diffraction efficiency is defined as the fraction of power in the
desired orders over the power sum of all orders.
Under the condition that the optimization procedure locates the
global optimum of the problem, the completeness of the Fourier
series expansion guarantees that,
for 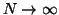 , the method converges to the best possible phase
grating that can be built to produce a given diffraction pattern!
Whether this condition can be fulfilled depends on the complexity of
the problem. In the case of simple one-dimensional problems
(
, the method converges to the best possible phase
grating that can be built to produce a given diffraction pattern!
Whether this condition can be fulfilled depends on the complexity of
the problem. In the case of simple one-dimensional problems
(
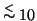 beams) we are confident that we find the global
optimum for two reasons:
beams) we are confident that we find the global
optimum for two reasons:
- low order diffraction beams correspond to slow variations of the
field along the
grating unit cell and can, therefore, be modeled very accurately with
a small number of Fourier coefficients.
- if the number of Fourier coefficients is not too large, the
random search for starting values can sample the parameter space very
densely, which makes it extremely unlikely to miss the global minimum.
In these simple cases a small number of Fourier
coefficients is generally sufficient to yield a good approximation of the
desired pattern and, since only a small number of parameters need to be
optimized, the algorithm is quite fast. Also, the convergence for
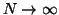 usually is very rapid. In
the following section we will present the numerical results for some
grating structures.
usually is very rapid. In
the following section we will present the numerical results for some
grating structures.


Next: Grating Performance
Up: Fourier Gratings as Submillimeter
Previous: Introduction
Urs Graf
2001-11-06
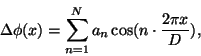
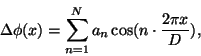
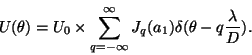
![]() the phase modulated field in the grating plane can be written as a
product of fields modulated by the individual Fourier components:
the phase modulated field in the grating plane can be written as a
product of fields modulated by the individual Fourier components:
![\begin{displaymath}
U_0\exp[ i\Delta\phi(x)] = U_0\prod^N_{n=1} \exp[ i a_n
\cos(n\cdot\frac{2\pi x}{D})] .
\end{displaymath}](img18.gif)
![]() of the phase modulation
defines a set of complex coefficients
of the phase modulation
defines a set of complex coefficients ![]() , each of which
describes the field in one diffraction order of the grating. Since we
are only interested in the intensity distribution within the
diffraction pattern, our task consists of finding a set of
, each of which
describes the field in one diffraction order of the grating. Since we
are only interested in the intensity distribution within the
diffraction pattern, our task consists of finding a set of ![]() , which
produces the desired set of
, which
produces the desired set of ![]() . For our standard example -- a
one-dimensional grating producing a symmetric pattern of four beams
-- this set is
. For our standard example -- a
one-dimensional grating producing a symmetric pattern of four beams
-- this set is
![]() .
.
![]() , the method converges to the best possible phase
grating that can be built to produce a given diffraction pattern!
Whether this condition can be fulfilled depends on the complexity of
the problem. In the case of simple one-dimensional problems
(
, the method converges to the best possible phase
grating that can be built to produce a given diffraction pattern!
Whether this condition can be fulfilled depends on the complexity of
the problem. In the case of simple one-dimensional problems
(
![]() beams) we are confident that we find the global
optimum for two reasons:
beams) we are confident that we find the global
optimum for two reasons:
![]() usually is very rapid. In
the following section we will present the numerical results for some
grating structures.
usually is very rapid. In
the following section we will present the numerical results for some
grating structures.