A new entropy stable magnetohydrodynamic solver for astrophysical purposes
Most astrophysical processes such as molecular cloud or star formation span too many temporal and spatial scales and are unsuitable for laboratory experiments. To overcome these limitations, computational astrophysics has evolved as a modern field of research using complex computer simulations to gain insight into physical processes. Its core task is to deliver theoretical predictions where analytic models can no longer be used to explain complex phenomena.
One major difficulty in astrophysical scenarios is the omnipresence of magnetic fields. There is strong evidence that magnetic fields play an important role in astrophysical processes. They have been observed on almost every scale from stars and planets to the interstellar medium up to galaxies (see, e.g., Beck, 2009; Crutcher, 2012; Haverkorn; 2015) and found to have energies comparable with the kinetic energies of the flows themselves (Naab & Ostriker, 2014).
Unfortunately, the ideal MHD equations, which are the most often used tool for simulating magnetized plasmas, have two important drawbacks. Firstly, they do not limit the growth of numerically caused magnetic field divergence errors. Furthermore, many numerical schemes are not conformable with the second law of thermodynamics, also known as the entropy inequality.
It seems mandatory to be able to guarantee not only a thermodynamically consistent fluid behavior but also to ensure that the magnetic field divergence stays low as mandated by Gauß's law ($\nabla\cdot\vec{B}=0$). Accordingly, we recently developed a new thermodynamically consistent numerical scheme for the simulation of plasmas under extreme conditions as found in astrophysical contexts (see, e.g., Derigs et al., 2018a,b).
In agreement with earlier publications, we call this scheme the "entropy stable ideal GLM-MHD" equations.
First numerical results confirm the utility and robustness of our new numerical scheme. It is applicable to state-of-the-art simulations (see figure). It can equally well be used for simulations with and without magnetic fields and resolves fluid features accurately.
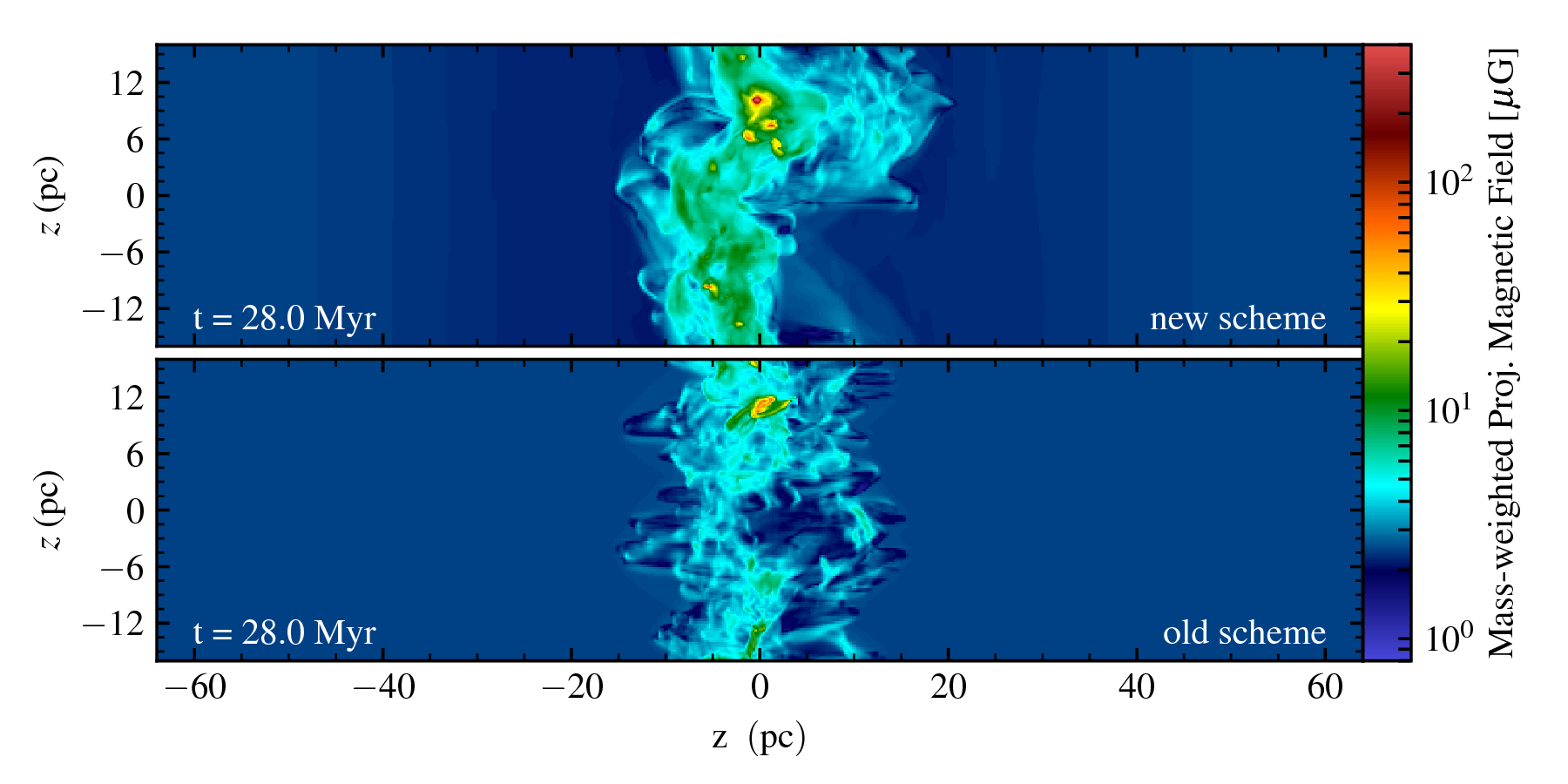
(bottom) Projection plot of the magnetic field strength in the colliding flow setup. As can be seen, the mean magnetization is notably higher in the solution obtained using our new scheme. This is in agreement with reference solutions computed using constrained transport (CT) methods. As CT schemes are much more computationally intense, they are in general unsuitable for computing multi-physics simulations as we aim to do.