VIRIAL ANALYSIS OF MOLECULAR CLUMPS FORMING IN COLLIDING FLOWS

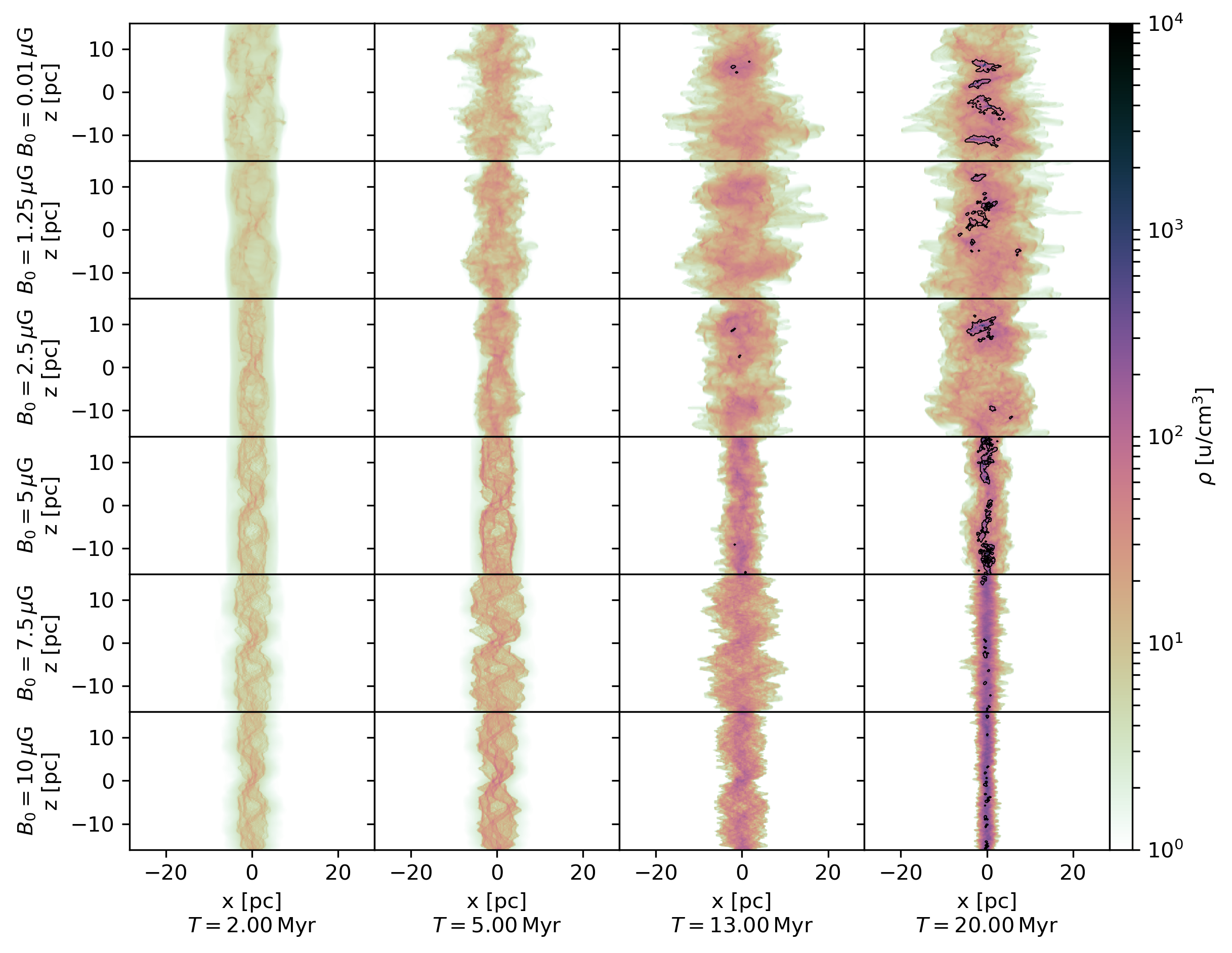
Understanding the structural and chemical evolution of turbulent molecular clouds is an essential part in understanding the star formation process. The formation and evolution of molecular clouds is investigated in a setup of magnetized colliding flows modelled by the 3D AMR code FLASH. The setup includes a basic chemistry model (Nelson & Langer 1997), which allows us to track the chemical evolution of important gas species (H1, H+, H2, C+, CO) involved in the formation process. We then identify molecular clumps in a set of simulations differing in the initial magnetic field strength by applying a CO abundance threshold and a friends-of-friends alike neighborhood linking algorithm suited to process adaptive mesh refined data (top figure).
Full evaluation of the components of the Eulerian virial theorem (Dib et al. 2007) allows us to assess the virial balance of the clumps. This involves the calculation of their kinetic-, thermal- and magnetic volume energies and the corresponding surface energies, their potential energy and the time dependence of the flux of inertia through their surface. The results show that the surface energy terms plays an important role, as they are often of the same order of magnitude compared to the corresponding volume energy terms. Furthermore, it indicates that the total virial balance of the molecular clumps in our simulations is often dominated by the time dependent $\Phi$-term, which hints at the evolution of their radial mass distribution to be influenced by accretion onto their surface (bottom figure).
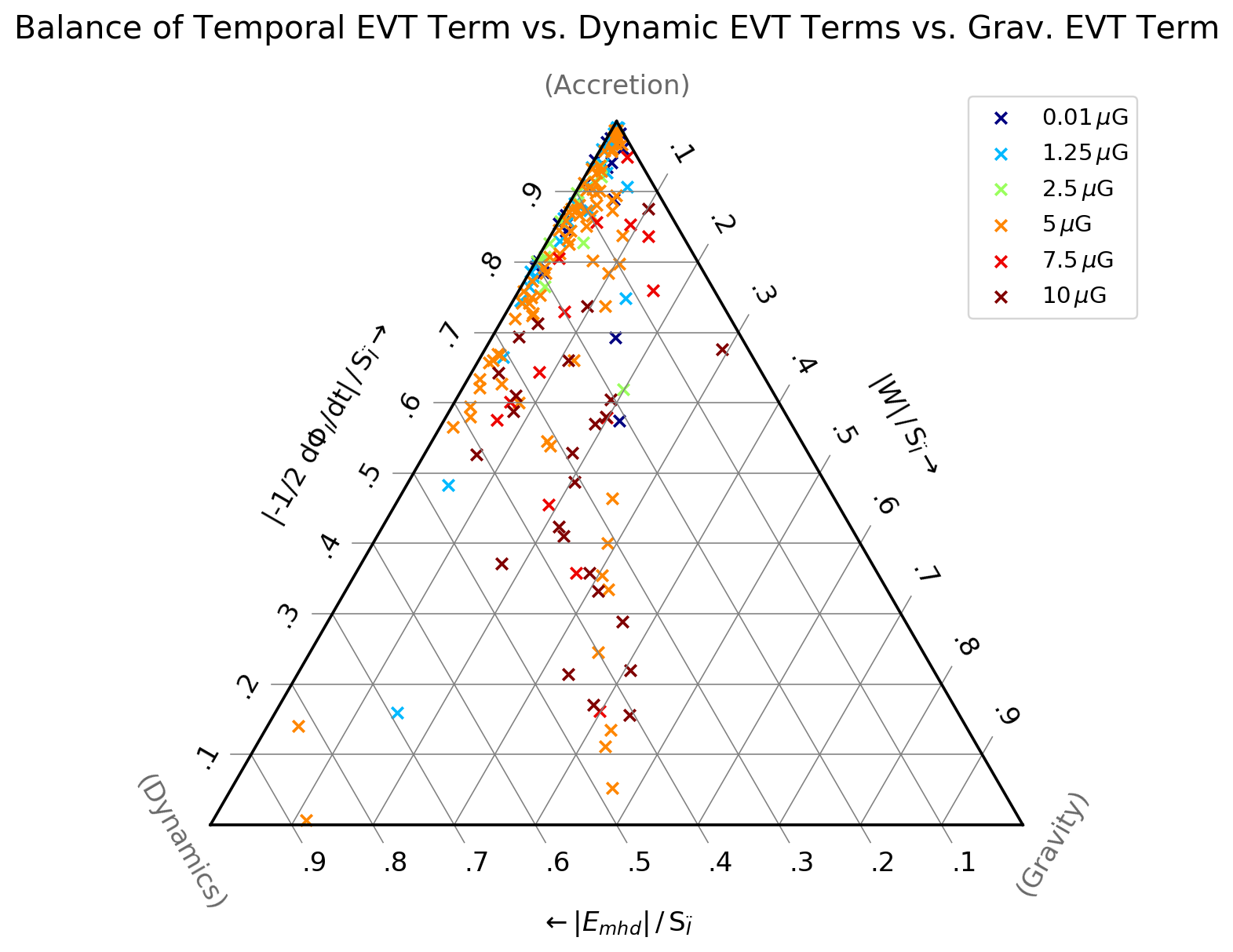
Los Angeles

Los Angeles
Figure: (top) Edge-on maps of the simulations column average density at 2, 5, 13 and $20\,\text{Myr}$. The displayed simulations have initial ambient magnetic fields $B_0$ of $0.01\,\mu\text{G}$, $1.25\,\mu\text{G}$, $2.5\,\mu\text{G}$, $5\,\mu\text{G}$, $7.5\,\mu\text{G}$ and $10\,\mu\text{G}$. The black contours indicate the identified clumps.
(bottom) Ternary diagram comparing the absolute values of the terms. in the Eulerian virial theorem, evaluated for clumps detected at 20 Myr. $E_{mhd}$ is the sum of the thermal, kinetic and magnetic energy, $W$ is the potential energy due to self-gravity and $\Phi$ is the flux of moment of inertia through the surface. For many clumps, the time-dependent $\Phi$-term dominates.