Symmetric Gratings

Our primary driver for the development of these gratings is their usage as local oscillator beam multiplexer in heterodyne receivers beyond 500 GHz. We, therefore, present a selection of gratings that produce a given number of equally strong diffraction orders. Our standard case is the production of four equal beams. Dammann gratings for this application are notoriously inefficient, since only $\approx$70% of the incident power emerges in the 4 central diffraction orders.

In the simplest version of a 4-beam grating, the beams are located symmetrically with respect to the 0$^{\rm th}$ diffraction order. In this case, and whenever an even number of beams is required, it is important to suppress all the even diffraction orders. This can be achieved with a phase grating by introducing a half wave phase step in one half of the unit cell. This phase step is quite naturally found by our optimization algorithm.

Figure 1: Comparison of the grating structure (upper panels) and the diffraction patterns (lower panels) for three different numbers of Fourier coefficients.

Figure 2: Diffraction efficiency of a Fourier grating plotted against the number of Fourier coefficients. The coefficients were optimized to produce 4 identical beams in the diffraction orders -3, -1, +1, and +3. The dashed line gives the maximum efficiency achieved with $N=99$ coefficients.

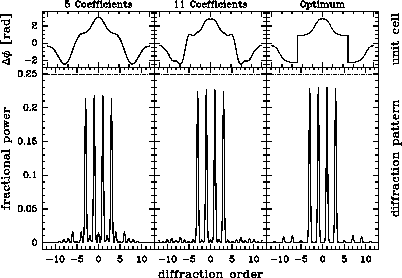
In Fig. 1 we show optimized grating structures and diffraction patterns for different numbers $N$ of Fourier coefficients. It is evident how the structure approximates the half wave phase step and for large $N$ converges to the optimum grating which is composed of a smooth "hump" overlaid on the step function. It is also clear that the structures composed of small numbers of Fourier coefficients represent a fairly crude approximation of this optimum function, but nonetheless diffract almost as much intensity into the four central beams as the optimum grating. Although the $N = 11$ grating reaches more than 98% of the maximum efficiency, its structure is still very smooth. This is the reason, why these gratings are so well suited for direct two-dimensional milling. The sharp phase steps required to perfectly suppress even diffraction orders, are not really necessary to produce a high efficiency in a four beam grating. It is sufficient to approximate this step rather coarsely, since the power lost into the even orders is partly compensated for by power gained from the odd orders.

Figure 3: Efficiency of Fourier gratings producing a given number of equal beams. The dotted line marks the maximum efficiency achievable with $N=5$ Fourier coefficients, the solid line gives the efficiencies for $N\to \infty$.

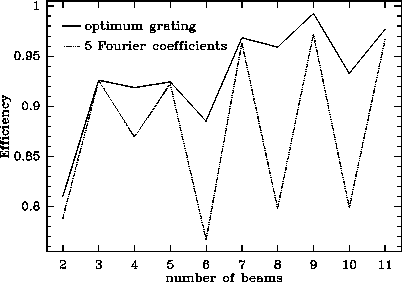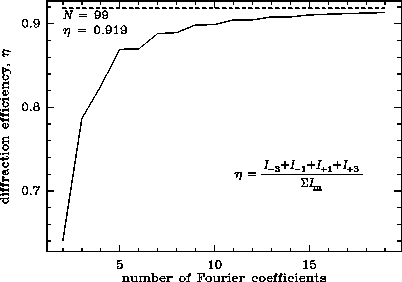
Fig. 2 shows how the efficiency of the 4-beam grating improves with the number of Fourier coefficients. The efficiency converges very rapidly to the optimum of 0.919. For $N>5$ the efficiency improvement is almost exclusively due to the odd Fourier coefficients. These are the coefficients required to approximate the half wave phase step. For the approximation of the structure on top of the phase step, the first two even coefficients are basically sufficient.

Table I: Fourier coefficients of 5 coefficient Fourier gratings producing $M$ equally intense beams. The bottom fraction of the table gives the coefficients for even numbers of $M$ when the half wave phase step is imposed separately instead of through the Fourier series expansion. $\eta$ denotes the theoretical grating efficiency.

$M$		$\eta$		.	$a_1$		.	$a_2$		.	$a_3$		.	$a_4$		.	$a_5$		.
2			0	.	789	1	.	975	0	.	000	-0	.	589	0	.	000	0	.	256
3			0	.	926	1	.	379	0	.	000	-0	.	217	0	.	000	0	.	057
4			0	.	870	1	.	965	0	.	997	-0	.	608	0	.	339	0	.	320
5			0	.	923	1	.	686	0	.	000	0	.	630	0	.	000	0	.	082
6			0	.	767	1	.	954	0	.	083	-0	.	625	1	.	324	0	.	314
7			0	.	964	1	.	225	1	.	253	-0	.	391	0	.	187	-0	.	022
8			0	.	798	2	.	020	2	.	864	-0	.	611	-0	.	660	0	.	436
9			0	.	972	2	.	932	0	.	762	-0	.	412	0	.	317	-0	.	168
10			0	.	799	1	.	923	2	.	555	-0	.	623	1	.	783	0	.	349
11			0	.	967	2	.	568	0	.	947	0	.	466	-0	.	510	0	.	546
2			0	.	810	0	.	000	0	.	000	0	.	000	0	.	000	0	.	000
4			0	.	919	0	.	983	0	.	322	0	.	023	-0	.	042	-0	.	029
6			0	.	878	1	.	919	-0	.	298	-0	.	008	0	.	370	-0	.	060
8			0	.	958	1	.	930	-0	.	707	-0	.	459	-0	.	152	-0	.	109
10			0	.	906	0	.	596	0	.	460	1	.	216	-0	.	209	-0	.	332

This is also seen in Fig. 3 where we show efficiencies for gratings producing various numbers of equally intense diffraction orders. For an odd number of beams, 5 coefficients are enough to reach to within a few percent of the maximum efficiency. For an even number of beams, more coefficients are required to get a high efficiency. The most important conclusion from Fig. 3 is that all these efficiencies reach $\approx$90% or more for a large enough number of Fourier coefficients. The 9-beam grating loses less than 1% of the power to higher diffraction orders. This illustrates that the Fourier gratings offer us a simple way to design and produce very efficient beamsplitters or similar devices.

As a reference, in Table I we list the coefficients for a selection of beam splitting Fourier gratings optimized with 5 Fourier coefficients. For the second part of Table I we added a periodic step function to the phase shift. In this way the Fourier series only has to model the phase variation within half a unit cell, and the expansion of the step function disappears. Thus the 5 coefficients listed in the table correspond to the first 5 even coefficients of the complete series.